Why bigger is not only bigger

Submitted by editor on 28 April 2015.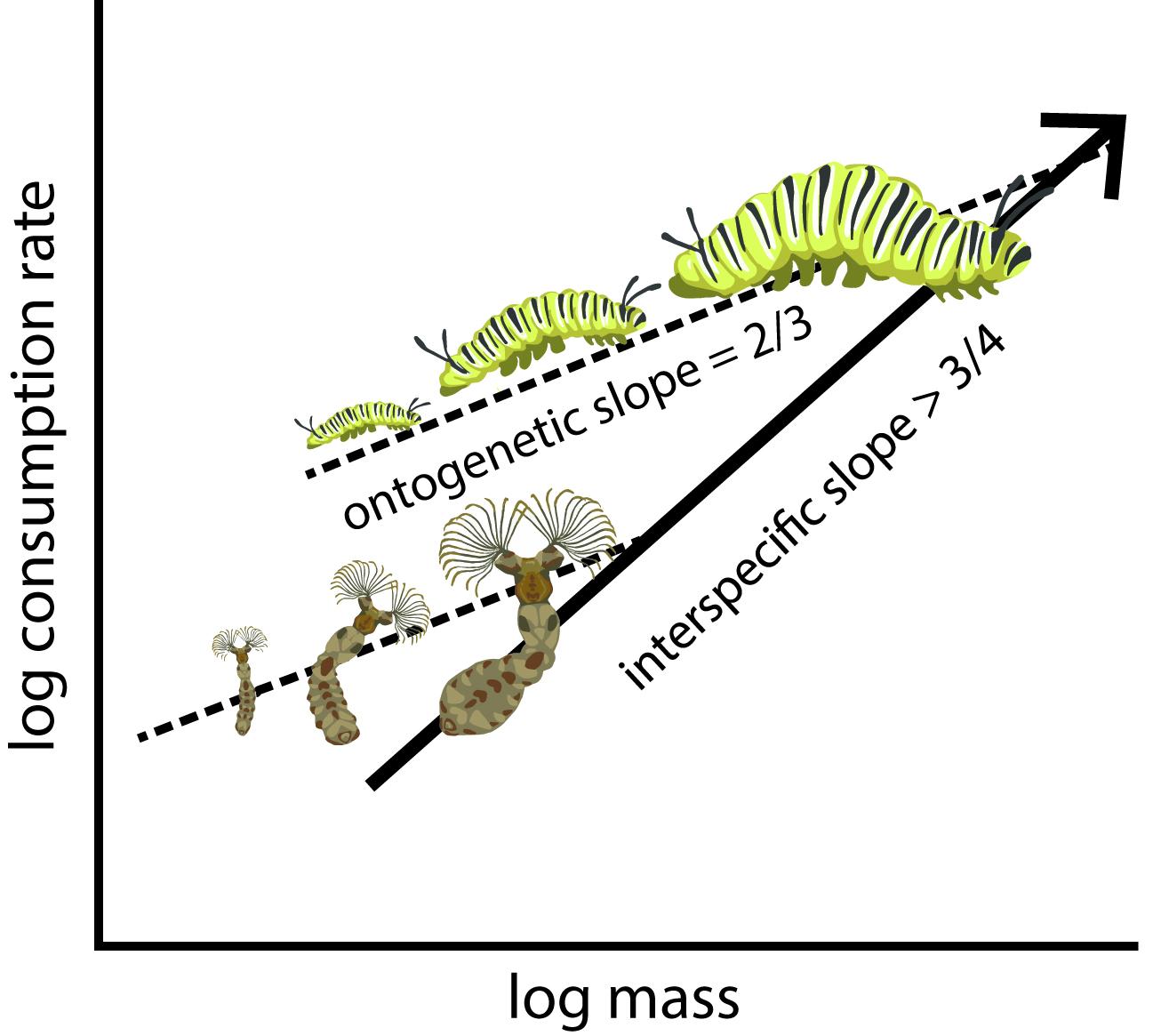Get the paper!

 

The study of scaling is an attempt to understand why bigger is not only bigger. A big cello produces a lower pitched sound than a small violin. A large cup of hot water will cool more slowly than a small one. When the size of a bridge is increased, the design must change to compensate for its diminishing strength. Size imposes physical constraints on design. In biology, these physical constraints are relevant to understanding the way in which organisms are designed. Like the cello and the violin, acoustic principles explain the pitch difference between a lion’s ‘roar’ and cat’s ‘meow’ (Hast 1989). Euclidean geometry helps us understand why a small cup cools quickly and how a polar bear’s large thermal inertia facilitates surviving the harsh conditions of the arctic (Schmidt-Nielsen 1984). The same physics used by engineers to ensure bridges do not collapse explains why an ant can support 5000 times their body weight (Nguyen et al. 2014).

The physical principles underlying other scaling relationships are less transparent. One relationship of particular interest is the scaling of metabolic rate. Metabolic rate is the rate at which organisms process energy and materials to fuel life processes such as growth and reproduction. With energy and mass conservation being one of the few laws that penetrates all spatial and temporal scales of biology, metabolic rate is a fundamental rate of life. Organism metabolism constrains life processes spanning molecules to ecosystems, including DNA mutation rates (Gillooly et al. 2005), individual reproduction rates (Hamilton et al. 2011), population growth rates (Brown et al. 2004), and ecosystem carbon cycling (Brown et al. 2004).  Curiously, when metabolic rate (y) is expressed as an allometric function (y = aMb) of body mass (M), where a is the normalisation constant, the estimated exponent b does not indicate volumetric scaling (b = 1) or surface-area scaling (b =2/3) but, for diverse organisms, tends to take an intermediary value close to a ¾ (Isaac and Carbone 2010).

While much intellectual effort has been directed at uncovering the possible principles driving metabolic scaling, there is still much debate on the topic. Much of this disagreement is fuelled by observations that the scaling of metabolic rate is subtly dependent of a range of factors, including, which taxa are compared, the activity state, or the organisms’ temperature (Weibel et al. 2004, Glazier 2006, Isaac and Carbone 2010). Recently, we showed that metabolic scaling is even qualitatively different depending of the life stage (e.g. embryo, or feeding immature) (Maino and Kearney 2014). Given the large variety of influencing factors it seems biologist are not only tasked with explaining why metabolic rate scales roughly with mass raised to ¾, but also the many exceptions to this rule. Theory may be of use here (Maino et al. 2014).

The body-size of individuals is altered ontogenetically (via growth) and interspecifically (via evolution). In our recent study (to appear in Oikos) we show that there are sound theoretical reasons why these two mechanisms for size alteration have different effects on the expected scaling relationship. Using data on insect consumption rates during growth we discover systematic variation in scaling exponents. Interspecific comparisons generally lead to the estimation of higher exponents compared with ontogenetic comparisons. This is important for many other scaling studies that do not make the important distinction between ontogenetic and evolutionary size changes. Our results highlight the usefulness of theory combined with appropriate empirical tests to help resolve the controversy of metabolic scaling.      

The authors through James Maino

References

Brown, J. H. et al. 2004. Toward a metabolic theory of ecology. - Ecology 96: 858–73.

Gillooly, J. F. et al. 2005. The rate of DNA evolution: effects of body size and temperature on the molecular clock. - Proc. Natl. Acad. Sci. U. S. A. 102: 140–5.

Glazier, D. S. 2006. The 3/4-Power Law Is Not Universal : Evolution of Isometric , Ontogenetic Metabolic Scaling in Pelagic Animals. - Bioscience 56: 325–332.

Hamilton, M. J. et al. 2011. Universal scaling of production rates across mammalian lineages. - Proc. Biol. Sci. 278: 560–6.

Hast, M. H. 1989. The larynx of roaring and non-roaring cats. - J. Anat. 163: 117–121.

Isaac, N. J. B. and Carbone, C. 2010. Why are metabolic scaling exponents so controversial? Quantifying variance and testing hypotheses. - Ecol. Lett. 13: 728–35.

Maino, J. L. and Kearney, M. R. 2014. Ontogenetic and Interspecific Metabolic Scaling in Insects. - Am. Nat. 184: 695–701.

Maino, J. L. et al. 2014. Reconciling theories for metabolic scaling. - J. Anim. Ecol. 83: 20–9.

Nguyen, V. et al. 2014. The exoskeletal structure and tensile loading behavior of an ant neck joint. - J. Biomech. 47: 497–504.

Schmidt-Nielsen, K. 1984. Scaling, why is animal size so important? - Cambridge University Press.

Weibel, E. R. et al. 2004. Allometric scaling of maximal metabolic rate in mammals: muscle aerobic capacity as determinant factor. - Respir. Physiol. Neurobiol. 140: 115–32.

Insights into Oikos papers

Comments